Trigonometric equation and graphing (Test)
angles in standard position
the arrows in initial and terminal arms are optional
rotation angles (greater than 360°
coterminal, reference (positive acute angle), quadrantal angles: n π 2 n ∈ Z
Coterminal angles - angles in standard positions (if the vertex of the angle is at the origin of the x-y plane and its initial arm lies along the positive x-axis) with the same terminal arm
Positive angle sketched counterclockwise, negative sketched clockwise
Principal angle (0, 360 °
Reference angle (0, 90 ° θ
Quadrantal angle - any angle whose terminal arm is on either the x- or y-axis
evaluating trig ratios and finding unknown angles
Primary trigonometric ratio
SOH: s i n θ hypotenuse
CAH: c o s θ
TOA: t a n θ
when calculating the ratios
put the negative signs in front of the entire fraction
keep the x, y, r, all positive when calculating the reference angles, and then later add the negative sign in brackets if needed
if using the scientific calculator, make sure the calculator is in the degree mode and align the manual calculation
beware of the range of θ
beware of the domain of θ 360 °
ex. s i n θ s i n − 1 ( 0.642 )
note radian/degree units in the final answer
CAST system: acronym denoting which quadrants the ratios among sin, cos, tan are are (is) positive, in the order of Quadrant 4,1,2,3
arc length (a=rθ r 2 θ 2
graphing
all roots on the graph : the x-coordinates of all x-int points, note to only add the ones on the graphDesmos graphing online can be used to check the shapeAmplitude cannot be negative = m a x − m i n 2
Vertical displacement = m a x + m i n 2
Phase shift - special name for the horizontal translation of a sinusoidal function; + right, - left
Shift & displacement both needed to be conducted at the last as in function translation when graphing
problem solving
if not marked specifically, 1 unit on the square means 1
Sinusoidal function graphing, don't come up too steep
read the question clearly, like number of periods etc. requirement for sketching
include a conclusion statement
only round in the final answer
when converting, don't forget to add the ° beware of the Calculator mode: degree - radian
θ θ × π 180 °
Identities (Test)
Test: Monday 04.17
Proofs (2)
Simplifying (1)
Solving (2)
Find an exact value of a trig ratio (2)
reciprocal trig ratios:
c o t θ = 1 t a n θ s e c θ = 1 c o s θ c s c θ = 1 s i n θ
quotient identities
Pythagorean identities
s i n 2 θ + c o s 2 θ = 1 1 + t a n 2 θ = s e c 2 θ c o t 2 θ + 1 = c s c 2 θ
addition identities
c o s ( A + B ) = c o s A c o s B − s i n A s i n B s i n ( A + B ) = s i n A c o s B + c o s A s i n B t a n ( A + B ) = t a n A + t a n B 1 − t a n A t a n B
Strategies to simplify a trig expression
get a common denominator
factor
change terms to sine or cosine
multiply the numeral and denominator both with a conjugate binomial
5 + 2 5 − 2
double angle
s i n ( 2 x ) + 1 = ( c o s ( x ) + s i n ( y ) ) 2 c o s ( 2 x ) = c o s 2 ( x ) − s i n 2 ( x ) = 2 c o s 2 ( x ) − 1 = 1 − 2 c o s 2 ( x )
when combining restrictions, beware not to miss any sub-restrictions by testing with a full rotation
when proving identities, start simplifying with the side identified to be more complicated
LCD = lowest common denominator
QED = Latin, meaning which was to be demonstrated
double cross for fractions equations
Others
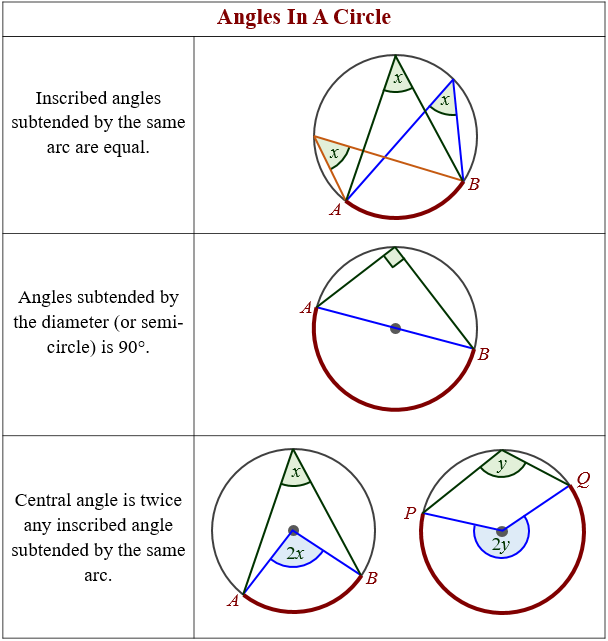
Angles in a Circle
Central angle is twice any inscribed angle subtended by the same arc
Inscribed angles subtended by the same arc are equal - angles in the same segment theorem: angles in the same segment are equal
Angles subtended by the diameter is 90 °
Cyclic quadrilateral: the opposite angles in a cycle
Use height of the triangle to prove
Law of sines: a sin ( α ) = b sin ( β ) = c sin ( γ ) = 2 R
R is the radius of the triangle's circumcircle
Law of cosines: c 2 = a 2 + b 2 − 2 a b cos ( γ )
Others
s i n 2 θ + c o s 2 θ = 1 s i n ( α + β ) = s i n α c o s β + c o s α s i n β c o s ( α + β ) = c o s α c o s β − s i n α s i n β t a n ( α + β ) = t a n α + t a n β 1 − t a n α t a n β
angular measure
trigonometric ratio
solving trigonometric equations
algebraic method using calculator
ambiguous case (SSA)